The same amount of energy is lost in an RC circuit no matter how small R is made

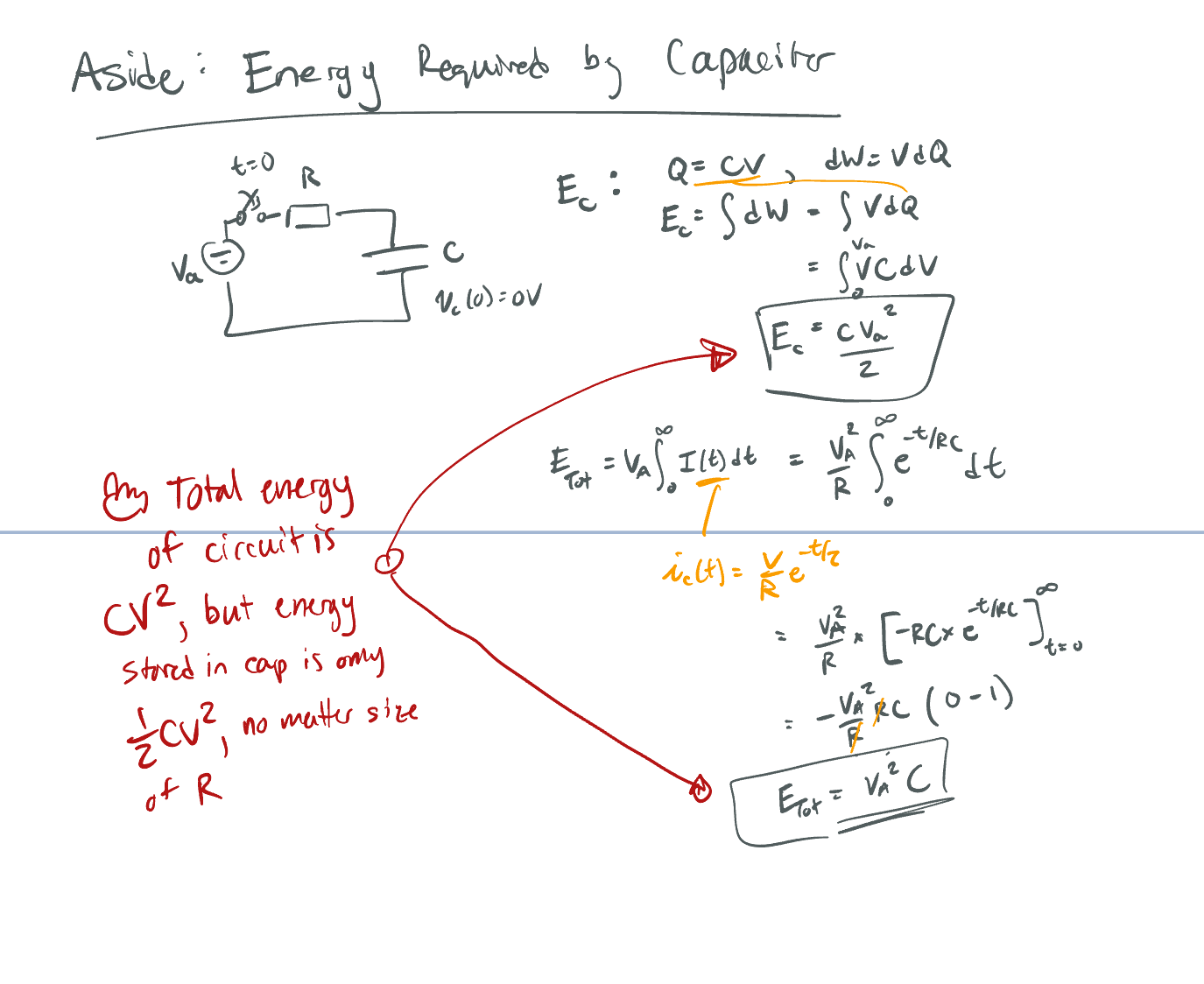
The energy required (from e.g. a battery) to charge a capacitor from 0 to $V_A$ is $E=C{V}_A^2$, but the energy stored by the capacitor is only $E_C=\frac{1}{2}C{V}_A^2$.

This is important for digital circuits, since every time we switch an output from 0 to 1 we have to charge the line capacitance up to $V_{DD}$, thus we use up $C{V}_{DD}^2$, and on the discharge we don’t use up any energy from the supply.

Also note that $\frac{1}{2}C{V}^2$ is dissipated at each switching occurrence, since of course the stored energy in the line capacitance must be discharged somewhere - this is important for thermal considerations especially at high speeds.

Hyperphysics notes that even if we decrease R toward 0, the current charging the capacitor grows large and thus $P_{dis}=I^{2}R$ is also large. For high speeds there is a point when this energy is not dissipated by the resistor but radiated as electromagnetic radiation — there is still no free lunch and we only get $E_C=\frac{1}{2}C{V}^2$ into the capacitor but use up $E=C{V}^2$ from the power source.

A simplified “proof” is shown below, note that the R term drops out of the $E_{Tot}$ equation: