The black magic of noise shaping in Sigma-Delta ADCs

The “noise shaping” function of a Sigma-Delta ADC seems like black magic at first, but in the end it is just actual black magic.

Oversampling is easy to understand — we have a set amount of quantization noise given by the quality of the ADC (which has an upper ideal limit) and by oversampling we spread the sampled noise over a larger bandwidth and then remove much of this noise with a low pass filter.

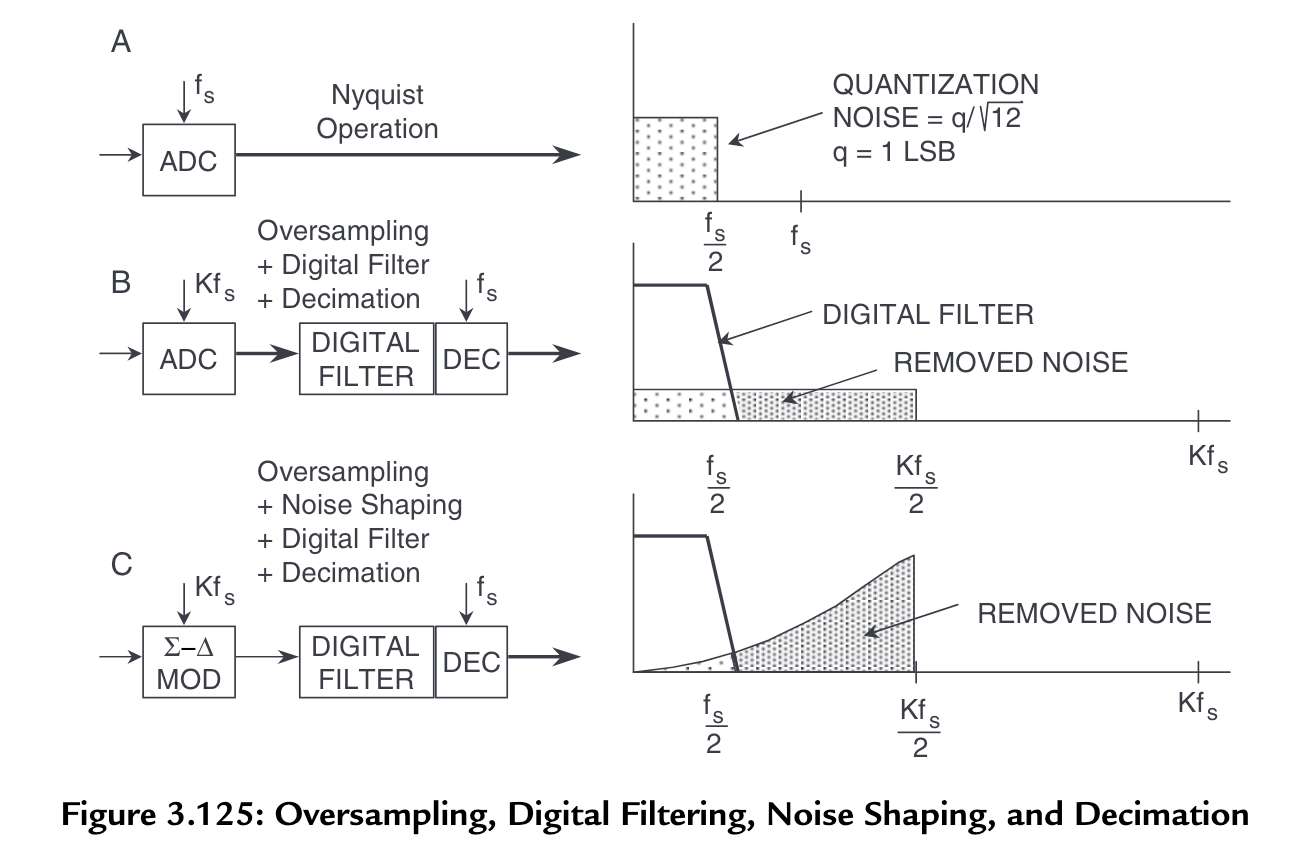
But what is this noise shaping? Shown in (C) above [1], we somehow are able to shape the quantization noise itself. If we look at the block diagram we can see how this works using hand-wavy systems math in the frequency domain.

The integrator used in the Sigma-Delta converter is represented in the frequency domain as 1/f. The input is X and the output is Y, but we also include our quantization noise as constant Q which is added after the integrator (i.e. before the sample is taken). Y is then fed back and subtracted from the input.

We can see that the function describing this is

$$\begin{array}{rl}Y& =\frac{1}{f}(X-Y)+Q\\ Y(1+1/f)& =X/f+Q\\ Y& =\frac{X+Qf}{1+f}\\ Y& =\frac{X}{1+f}+\frac{Qf}{1+f}\end{array}$$

Then we can see that one term depends on the input X and other depends on the quantization noise Q. For $f\to 0$ the signal term goes to X and the Q-noise term drops out. For $f\to \infty$ the Q-noise term is all that is left. So in effect we have done some magic to push our quantization noise to higher frequencies and leave our signal in tact for lower frequencies.

Note the MT-022 Tutorial is an extract of the book in [1] which explains this more in depth.

[1] Kester, W. (Ed.). (2005). The Data Conversion Handbook. Newnes. ISBN 0-7506-7841-0.